0.1.1 标准库之 find 和 find_if 函数

• find_if()

1 find()

C++ 标准库中的 find，find_if 函数可以用于对数组、容器等进行查找。
http://www.cplusplus.com/reference/algorithm/find/

头文件

很多人对二分感到很苦恼，很困惑，可能是因为二分的边界很难掌握，也许是判断条件难写…

然而，很幸运，你找到了这篇文章，仔细看下去，这篇文章将带你学透二分！！！

二分可以简单分为二分查找与二分答案。

可能你听说过二分查找，二分查找和二分答案是不是一回事呢？答案是否定的。二分查找只是单纯的查找就可以了，简单的控制好边界条件。而二分答案也许稍复杂些。

首先，我们看一下二分的模板：

二分法相信大家都会，它最基本的应用是求一个单调函数的零点。

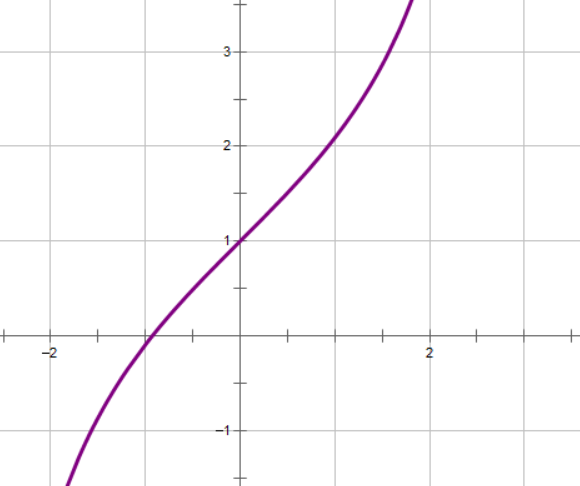三分法是二分法的变种，他最基本的用途是求单峰函数的极值点。

![[../../../images/Z-attachment/Pasted image 20231118201007.png]]

从数学的角度来说，求极值点，先求导再二分不就好了吗？然而，实际中我们遇到的函数，求导可能很困难，所以会用上三分法。而三分法的原理非常简单，以求极大值为例，每次对一个区间[l,r]求三等分点lsec和rsec：

• 如果f(lsec) < f(rsec) ，说明极大值一定在[lsec,r]内取到，因为如果在[0,lsec)内，那rsec一定处于单调下降的区间内，它的函数值不可能大于lsec的函数值。 于是我们令l=lsec并继续。

史上最全的 C++ STL 容器大礼包

为什么 C++\(C++\)比 C\(C\)更受人欢迎呢？除了 C++\(C++\) 的编译令人感到更舒适，C++\(C++\)的标准模板库（STL\(STL\)）也占了很重要的原因。当你还在用手手写快排、手写二叉堆，挑了半天挑不出毛病的时候，C++\(C++\)党一手 STL\(STL\)轻松 AC\(AC\)，想不嫉妒都难。

所以这篇随笔就带大家走进博大精深的 C++STL\(C++STL\)，系统讲解各种 STL\(STL\)容器及其用法、作用。在学习 STL\(STL\)的时候认真体会 STL\(STL\)语法及功能，提升自己在算法竞赛及程序设计中解题、码代码的能力。

话不多说，现在开始：

浅谈 C++ STL vector 容器

定义 带余除法 对于给定的任意整数 \(a,b\)a,b 其中 \(b>0\)b>0，存在唯一的整数对 \(q,r\)q,r 使得 \(a=bq+r\)a=bq+r 且 \(r\in [0,b-1]\)r。

证明用到良序原则（自然数的非空子集必然存在一个最小元素）。

先考虑存在性的证明。构造集合 \(S=\{a-bk|k\in \mathbb Z,a-bk\ge 0\}\)，那么必然存在一个最小元 \(r\) ，满足 \(a-qb=r,a=qb+r\) a-qb=r,a=qb+r。接下来证明 \(r<b\) r<b，这很显然，因为如果 \(r\ge b\) 则存在 \(r'=r-b\ge 0\) r'=r-b，也在集合 \(S\) 中，矛盾。接下来证明唯一性。由于 \(r\ge 0\) ，所以只存在唯一的 \(r\) r 满足 \(0\le r<b\) 0r<b，那么也就只有唯一 \(q\) 。

定义 整除

若 \(a=bq\)a=bq 则称 \(b\)b 整除 \(a\)a，记作 \(b\mid a\)ba。称 \(b\)b 是 \(a\)a 的约数。整除具有传递性。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

+-----------------+           +---------------+           +-----------------+
|   天然气公司    |----(1,n)- -|   监测地点    |-----(1,n)-|     计量表     |
+-----------------+           +---------------+           +-----------------+
| 公司编号(PK)    |           | 地点编号(PK) |            | 设备序列号(PK)  |
| 公司名称        |           | 纬度          |           | 编码口令        |
| 联系电话        |           | 经度          |           | 设备型号        |
| 联系人          |           | 名称          |           | 出厂日期        |
| 联系地址        |           | 备注          |           | ...             |
+-----------------+           | 安全负责人    |           +-----------------+
                             +---------------+
+-------------------+
| 测量数据包       |
+-------------------+
| 时间戳            |
| 设备序列号(FK)   |
| 温度              |
| 压力              |
| 电池电压          |
| 工况流量          |
| 累积流量          |
+-------------------+

天然气公司

监测地点

Preliminaries - SymPy 1.12 documentation 是官方教学文档 欢迎使用SymPy的文档！ — SymPy 1.8.dev 文档 中文的文档

1
2
3
4

from sympy import *
from sympy.abc import a,b,c,x,y
from matplotlib import rc
rc('text',usetex=True)

有很多时间的话我会学一学这个 \('\int\limits_{0}^{\pi} \cos^{2}{\left (x \right)}\, dx'\)

\(\{ \frac{3}{2} - \frac{\sqrt{17}}{2} : 1, \ \frac{3}{2} + \frac{\sqrt{17}}{2} : 1\}\)

Python 教程 — Python 3.12.0 文档

matplotlib.lines.Line2D — Matplotlib 3.8.2 documentation 官方教程 教程 | Matplotlib 中文文档