A. Square
给出四个坐标,算出正方形的面积 1
2
3
4
5
6
7
8
9int _,x[5],y[5];
void solve()
{
for (int i = 1; i <= 4;i++)
cin >> x[i] >> y[i];
sort(x + 1, x + 5);
sort(y + 1, y + 5);
cout << (x[4] - x[1]) * (y[4] - y[1]) << '\n';
}
B . Arranging Cats
科学家们有 \(n\) 个箱子,猫可以坐在里面,也可以不坐在里面。 盒子的当前状态用序列 \(b_1, \dots, b_n\) 表示:如果 \(i\) 号盒子里有猫,则为 \(b_i = 1\) ,否则为 \(b_i = 0\) 。
幸运的是,猫可以无限量生产,因此科学家们可以在一天内完成以下操作之一:
- 取一只新猫并将其放入盒子中(对于 \(i\) 中的 \(b_i = 0\) ,指定 \(b_i = 1\) )。
- 从盒子中取出一只猫,让它退休(对于 \(i\) 中的 \(b_i = 1\) ,指定 \(b_i = 0\) )。
- 将一只猫从一个盒子移到另一个盒子(对于 \(i, j\) 中的 \(b_i = 1, b_j = 0\) ,指定 \(b_i = 0, b_j = 1\) )。
我们还发现,有些盒子里马上就装满了猫。因此,科学家们知道猫在盒子中的初始位置 \(s_1, \dots, s_n\) 和期望位置 \(f_1, \dots, f_n\) 。
指出检验假设所需的最少天数。
对于每组数据: \(\boxed{\begin{array}&n\\s(string)\\f(string)\end{array}}\)
Solution
实际上,一对 \((0,1)(1,0)\)
可以相互抵消掉,则答案就是 可以抵消掉的对数 加上
不能抵消掉的对数 可以抵消的个数为 \(cnt=\min(cnt_{1},cnt_{2})\),没有抵消掉的个数为
\(max(cnt_{1},cnt_{2})-cnt\) 总数即为
\(max(cnt_{1},cnt_{2})\)
1 | string s, f; |
C . Sending Messages
需要在 \(m_1, m_2, \dots m_n\) ( \(m_{i}<m_{i+1}\) ) 时刻发送 \(n\) 条信息。 在 \(0\) 时刻,他的手机只剩下 \(f\) 单位的电量。在 \(0\) 时刻,手机处于开机状态。
每开机一个单位,手机就会损失 \(a\) 个单位的电量。 此外,斯捷潘可以随时关闭手机,稍后再打开。这一操作每次消耗 \(b\) 个单位的能量。 考虑到开机和关机是瞬时的,因此您可以在 \(x\) 时刻开机,并在同一时刻发送信息,反之亦然,在 \(x\) 时刻发送信息,并在同一时刻关闭手机。
如果在任何时刻电量降至 \(0\) (变为 \(\le 0\) ),则无法在该时刻发送信息。
由于所有信息对斯捷潘都非常重要,他想知道是否可以在不给手机充电的情况下发送所有信息。
给出
需要发送的信息数量、手机初始电量、单位时间电量消耗
以及 依次关机和开机时的电量消耗。
判断是否能够发送所有信息。 对于每组数据: \(\boxed{\begin{array}&n&f&a&b\\m_{1}&m_{2}&m_{3}&\dots&m_{n}\end{array}}\)
Solution
1 |
|
D . Very Different Array
给出 \(a,b\) 数组,分别有 \(n,m个整数(m\geq n)\),在 \(b\) 数组中选出 \(n\) 个数组成一个长度为 \(n\) 的新数组使得: \(D=\sum\limits_{i=1}^n\mid a_{i}-c_{i}\mid\) 最大并输出 \(\max(D)\)
对于每组数据: \[\boxed{\begin{array}&n&m\\a_{1}&a_{2}&\dots&a_{n}\\b_{1}&b_{2}&\dots &b_{m}\end{array}}\]
Solution
我的想法是最大减去对应的最小的,但是是错误的
Hack 数据 1
2
32 6
7 9
8 1 10 6 3 9
- \(a:7,9\)
- \(b: 10,9,8,6,3,1\)
- 大的减去对应小的: \(D=(10-7)+(9-1)=11\neq 12\) \(\Huge{WA}\)
expect 12
BUT found 11
一个正确的思路和我的很像却也不同:
- 当选定 \(n\) 个数的时候,只需要大的减去对应小的依次相加即可
- 一般中间的不取,只取前面 \(i\) 个和后面 \(n-i\) 个即可,(我做的时候是按照前面和后面均分来的,但是是错误的)
因此做法是:
确定一个界限 \(i\),先按照对应(大对应小)来计算
ans,后面只需要计算变化量即可。
可以枚举每一种情况 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23int a[200010], b[200010];
void solve()
{
int n, m;
cin >> n >> m;
for (int i = 1; i <= n; i++)
cin >> a[i];
for (int i = 1; i <= m; i++)
cin >> b[i];
sort(a + 1, a + n + 1);
sort(b + 1, b + m + 1, greater<int>());
long long ans = 0, tmp = 0;
for (int i = 1; i <= n; i++)
tmp += abs(a[i] - b[i]);
ans = tmp;
for (int i = 0; i < n; i++)
tmp += abs(a[n - i] - b[m - i]) - abs(a[n - i] - b[n - i]),ans = max(ans, tmp);
cout << ans << '\n';
}
E. Eat the Chip
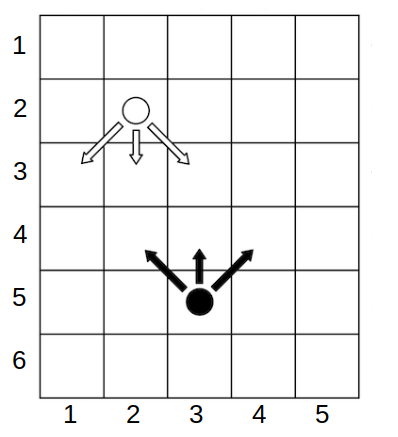
Alice(白) 和 Bob(黑)能走的方向如图。双方都以最佳状态下棋,结果是?
对于每个样例: \[\boxed{\begin{array}&h&w&x_{a}&x_{b}&y_{a}&y_{b}\end{array}}\]
Solution
如果有一方发现自己会输,就会想办法平局,分类讨论,较为麻烦
先算出两人见面之前 \(y\)
的范围,进攻方 \([l_{1},r_{1}]\),防守方
\([l_{2},r_{2}]\),满足:\(l_{1}\leq l_{2}+1,r_{1}\geq
r_{2}-1\),满足则可以 win,否则 Draw
1 | void solve() |
F. Sum of Progression
给你一个由 \(n\) 个数字组成的数组 \(a\) 。还有 \(q\) 个形式为 \(s, d, k\) 的查询。
对于每个查询 \(q\) ,求 \(a_s + a_{s+d} \cdot 2 + \dots + a_{s + d \cdot (k - 1)} \cdot k\) 即:
\[\large{\sum\limits_{i=1}^ka_{s+d(i-1)}\times i}\]
对于每个测试用例:\(\boxed{\begin{array}&n&q\\a_{1}&a_{2}&\dots&a_{n}\\s_{1}&d_{1}&k_{1}\\s_{2}&d_{2}&k_{2}\\\vdots&(q\ \text{query})\\s_{q}&d_{q}&k_{q}\end{array}}\)
Solution
根号分治 设置一个阈值: \[w=\sqrt{ n }\]
当 \(d>w\),直接暴力做(因为这时的运算次数很少了)
当 \(d\leq w\),开数组算前缀和. (\(s,d\text{分别代表}i,j\))
- \(f\) 数组来记录 \(\lfloor{\frac{s}{d}}\rfloor\times a_{s+\lambda \times d}\) 前缀和,记录的是 \(a_{s}\times \lfloor{\frac{s}{d}}\rfloor+s_{s+d}\times\lfloor{\frac{s+d}{d}}\rfloor+\dots\)
- \(g\) 数组记录的是 \(a_{s+\lambda \times d}\) 的前缀和,记录的是 \(a_{s}+s_{s+d}+\dots\)
- 差距 \(\left( \frac{s}{d}-1 \right)g=a_{s}\times\left( \frac{s}{d}-1 \right)+a_{s+d}\times\left( \frac{s}{d}-2 \right)+\dots\)
- \(\leftrightarrow\) \(\text{ans}=f-\left( \frac{s}{d}-1 \right)g=a_{s}\times1+a_{s+d}\times 2+\dots+a_{s+(k-1)d}\times k=\text{target}\)
- \(\leftrightarrow\text{ans=}\textcolor{green}{f[s+d\times(k-1)][d]-f[s-d][d]}-(\textcolor{grey}{g[s+d\times(k-1)][d]-g[s-d][d]})\times\left( \frac{s}{d}-1 \right)\)
处理方式可能不止一种...
1 | int n,q,a[100010]; |
G. Mischievous Shooter
谢尔只带了一把幸运猎枪,他可以朝四个方向之一射击:右下、左下、左上或右上。射击时,霰弹枪会击中所选方向上的所有目标,这些目标的曼哈顿距离不会超过一个固定常数
\(k\). 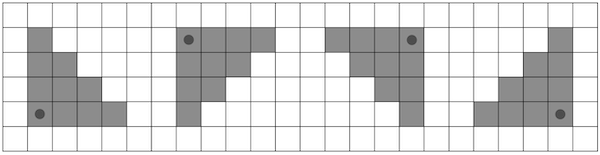
每个测试用例:
\(\boxed{\begin{array}&n&m&k\\str(m_{1})\\str(m_{2})\\\vdots\\str(m_{n})\end{array}}\) 其中字符". "表示单元格为空,字符 "#"表示存在目标.
输出一个整数,该整数等于一次射击击中目标的最大可能数目。
输入样例 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
194
3 3 1
.#.
###
.#.
2 5 3
###..
...##
4 4 2
..##
###.
#..#
####
2 1 3
#
#1
2
3
43
4
5
2
Solution
(待更...)