1925(921div2)

只做了一题，仍然是个废物 \(\dots\)，经过假期的训练，我希望达到至少过 3 题的水平

A. We Got Everything Covered!

给你两个正整数 \(n\) 和 \(k\) 。

您的任务是找出一个字符串 \(s\) ，使得所有可能的长度为 \(n\) 的字符串都可以用前 \(k\) 个小写英文字母作为 \(s\) 的子序列出现。

如果有多个答案，则打印长度最小的答案。如果仍有多个答案，可以打印其中任意一个。

注：如果从 \(b\) 中删除一些字符（可能为零）而不改变其余字符的顺序即可得到 \(a\) ，则字符串 \(a\) 称为另一个字符串 \(b\) 的子串。

void solve()
{
    int n, k;
    cin >> n >> k; // n:子字符串长度，k:字母个数
    vector<char> a;
    for (int i = 1; i <= n; i++)
        for (int i = 1; i <= k; i++)
            a.push_back('a' + i - 1);

    for (auto x : a)
        cout << x;
    cout << '\n';
}

B. A Balanced Problemset?

将 \(x\) 分解为 \(n\) 个整数组成，使得这 \(n\) 个数的 gcd 最大，也就是最平衡。

Solution

想了半天没想出来 \(\dots\)

没太搞懂 \(\dots\)

这段代码已经被 HACK 了，现在提交会 T

void solve()
{
    int n, x;
    cin >> x >> n;
    if (n == 1)
    {
        cout << x << '\n';
        return;
    }
    for (int i = x / n; i >= 1; i--)
    {
        if (x % i == 0 && x / i >= n)
        {
            cout << i << '\n';
            return;
        }
    }
}

有： \(GCD(a_1,a_2,a_3,\ldots,a_n) = GCD(a_1,a_1+a_2,a_1+a_2+a_3,\ldots,a_1+a_2+a_3+\ldots+a_n)\) \(\leftrightarrow GCD(a_1,a_1+a_2,a_1+a_2+a_3,\ldots,x)\)

所以答案一定是 \(x\) 的一个约数。

现在，考虑 \(x\) 的一个因数 \(d\)，我有两种想法 \((1)\)

当 \(n\times d\leq x\),选择为：\(d,d,d,\ldots,x-(n-1)d\leftrightarrow \gcd(d,2d,3d..,x)\) 有可行答案 \(d\)
当 \(n\leq d\),有可行答案 \(x//d\)（本来每一份是 \(\frac{x}{n},n\) 份，这时 \(n\leq d\)，如果分为 \(d\) 份每一份就是 \(\frac{x}{d}\) 可以分为更多份，每一份也更大，\(\geq n\) 的部分可以直接安到任意位置，这时的 \(\frac{x}{d}\) 也可以作为答案）

\((2)\)

直接遍历因子 \(1-x\) (然后 \(n\times d\leq x,取d\))会超时
遍历因子 \(1-\sqrt{ x }\) (然后 \(n\times d\leq x\ or\ n\times\left( \frac{x}{d} \right)\leq x,取d\ or\ x/d\)) 这样就可以将因子遍历完。

找到满足该条件的最大 \(d\)。这可以在 \(\mathcal{O}(\sqrt{x})\) 时间内通过简单的因数分解来实现。

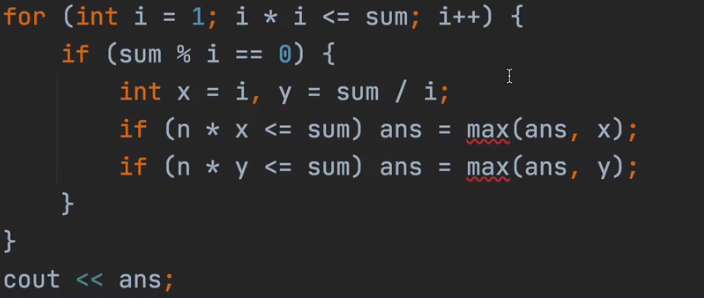
void solve()
{
    int n, x;
    cin >> x >> n;
    int ans = 1;
    for (int i = 1; i * i <= x; i++)
    {
        if (x % i == 0)//如果i是x的因子
        {
            if (n <= x / i)//n*i<=x ->i i i ... x-(n-1)*i  ->i
                ans = max(ans, i);
            if (n <= i)
                ans = max(ans, x / i);
        }
    }
    cout << ans << '\n';
}

C . Did We Get Everything Covered?

给你两个整数 \(n\) 和 \(k\) 以及一个字符串 \(s\) 。

您的任务是检查是否所有长度为 \(n\) 的字符串都可以用第一个 \(k\) 小写英文字母组成，并作为 \(s\) 的子序列出现。

如果答案是否定的，那么您还需要打印一个长度为 \(n\) 的字符串，该字符串可以用第一个 \(k\) 小写英文字母组成，但不会作为 \(s\) 的子序列出现。

如果有多个答案，您可以打印任意一个。

注：如果从 \(b\) 中删除一些字符（可能为零）而不改变其余字符的顺序，就可以得到 \(a\) ，那么字符串 \(a\) 就被称为另一个字符串 \(b\) 的子串。

(待更 \(\dots\))