1 数一数三角形
1.1 题目描述
在那遥远的角落三条边相拥相依它们相隔却又相连像爱情中的你我他 三角形有着神秘的力量让我们的爱情纯粹又完美无论相隔多远，相连多近爱，永远如三角形般美丽
你得到一个正 \(N\) 边多边形。将任意一条边标记为边 \(1\)，然后按顺时针顺序将下一条边标记为边 \(2\)、\(3\)、\(\dots\)、\(N\)。在 \(i\) 侧有 \(A_i\) 个特殊点。这些点的位置使得边 \(i\) 被分成长度相等的 \(A_i + 1\) 段。
您希望创建尽可能多的 满足条件的三角形，同时满足以下要求。 - 每个三角形由 3 个不同的特殊点组成（不一定来自不同的边）作为它的角。 - 每个特殊点只能成为最多 1 个三角形的角。 - 所有的三角形不能互相相交。 请你数一数可以创建的满足条件的三角形的最大数量。
1.2 输入
\(\boxed{\begin{array}&N\\ A_{1} &A_{2}& &\cdots& &A_{n} \end{array}}\)
数据范围: \(3 \leq N \leq 200\ 000\), \(1 \leq A_i \leq 2 \cdot 10^9\) ### 1.3 输出
输出一个整数，表示可以创建的三角形的最大数量。
1.4 示例 1
输入 1
24
3 1 4 61
4
1
23
1 1 11
1
1.6 说明
例如样例一，有一个正四边形。假设最上面的一条边被标记为边 \(1\)，下图显示了当 \(A = [3,1,4,6]\)
时特殊点如何位于每一边内及一种可行的方案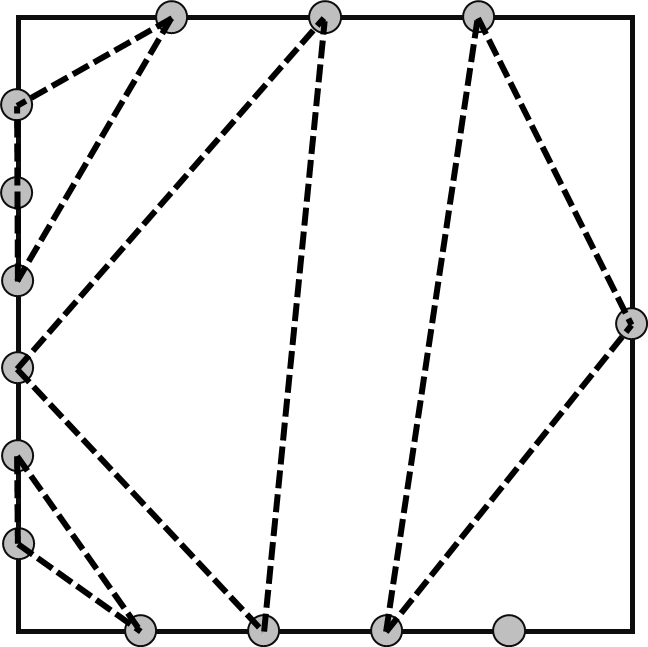 
### 1.7 代码 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
using namespace std;
ll n, a[200010];
int main()
{
cin >> n;
ll cnt = 0, maxa = 0;
for (int i = 1; i <= n; i++)
cin >> a[i], cnt += a[i], maxa = max(maxa, a[i]);
cout << min(cnt / 3, cnt - maxa) << '\n';
}
/*
ll ans = sum/3;
if (mx > 2 * (sum - mx)) {
ans = sum - mx;
}
cout << ans << endl;*/
有两个长度相等的字符串 \(a, b\) ,它们只包含字符 \(0\) 或 \(1\); 两个字符串都以字符 \(0\) 开始，以字符 \(1\) 结束。
您可以执行以下操作任意次数（可能为零）： - 选择其中一个字符串和两个相等的字符; 然后将它们之间的所有字符替换为这个字符。
即: 选择这两个字符串之一(假设为 \(s\))，然后选择两个整数 \(l\) 和 \(r\) ,满足 \(1\leq
l<r<\mid s\mid\) 且 \(s_{l}=s_{r}\) .然后替换在区间 \([l, r)\) 的所有字符 \(s_{i}\) ,使得 \(s_{i}\) 都替换为 \(s_{l}\) 。( \(\sum \limits_{i=l}^{r-1}s_{i}=s_{l}\)) ###
2.2 输入 > \(\boxed{\begin{align}&T\\&a_{1}
&b_{1}\\&a_{2} &b_{2}\\
&\vdots&\vdots\\&a_{T}&b_{T}\end{align}}\) >
>> \(T\)
为测试用例数量，每个测试用例由 \(a,b\)
两行组成 >> \(a,b\) 都以字符
\(0\) 开始，以字符 \(1\) 结束 > >数据范围 >> \(2\leq \mid a\mid=\mid b\mid\leq 5\ 000\) ,
\(1\leq T\leq 2\ 000\) >> \(\sum \limits_{i=1}^T\mid a_{i}\mid\leq 50\
000\) ### 2.3 输出
对于每个测试用例，如果可以使两个字符串相等，则打印
YES。否则，打印 NO。 ### 2.4 示例 输入
1
2
3
4
5
6
7
8
9
10
11
12
13
14
157
01010001
01110101
01001
01001
000101
010111
00001
01111
011
001
001001
011011
010001
0110111
2
3
4
5
6
7YES
YES
YES
NO
NO
NO
YES
2.6 代码
1 |
|
3
3.1 题目描述 ：
WZ 学长最近迷恋上了泡养生茶，他买了枸杞，决明子，菊花，栀子，桑葚，桑叶，蒲公英，金银花，茯苓，人参... 某天他突发奇想，是不是把两杯液体重量一样的养生茶倒到其中一个杯子里面再喝下去，就会获得双倍的效果还能少喝一杯茶！（智慧的眼神） 说干就干！假设 WZ 学长一共有 \(n\) 杯养生茶，每个杯子无限大并且初始只有 \(1\) 升养生茶。WZ 学长每次只会把两杯质量一样的茶倒进其中一个杯子（别问我为什么要一样多），而他每次最多只愿喝 \(m\) 杯，那么他最少还需要再调配多少杯养生茶。 （放心如果要喝的养生茶超过 \(1\) 升，那么 WZ 就会把多的都送给 Jiejie 学长并且看着他喝完！）
3.2 输入
\(\boxed{\begin{align}&n&m\end{align}}\) \(n\) 为 WZ 已有的养生茶杯数，\(m\) 为他愿意最多喝的养生茶数量
3.3 输出
输出一行最少还需要再买多少杯
3.4 样例
输入 3 1 输出 1 题解：二进制问题
1 |
|
4
4.1 题目描述 ：
WZ 最近想要学卷积神经网络了！但是因为这是他第一次做这种项目，于是乎，，，一个拥有数不清 bug 的屎山就诞生了! 虽心有余想要全部删了重构，然而项目就快要结题了，只好央求我们英俊潇洒风流倜傥的 Jiejie 学长来挽救于危难之间。Jiejie 虽然看不懂问题到底出在了哪里，但他发现 WZ 的 bug 出现的很有规律，每个 bug 只会影响当前行的代码，为了 debug 的舒服他决定数行数行的进行修改。于是他决定帮 WZ 重构 \(m\) 个片段（即从一个 bug 到另一个 bug 算一个片段），于是想问 Jiejie 学长最少需要重构多少行代码。
4.2 输入
\(\boxed{\begin{align}&x &n& &m\\&a_{1} &a_{2}& &\cdots &&a_{n}\end{align}}\) 第一行输入代码总长度 \(x\) 和 \(n\) 个 bug 以及 Jiejie 愿意重构 \(m\) 个片段数 第二行一共有 \(n\) 个数字代表每个 bug 的位置 数据范围： \(1\leq a_{i}\leq x\) \(1 \leq x,n,m\leq 1\ 000\) ### 4.3 输出 Jiejie 学长最少需要更改的行数
4.4 样例
输入 11 5 2 2 4 6 9 10
输出 5
题解：排序＋贪心 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
using namespace std;
int x,n,m;
int a[maxn];
int b[maxn];
int ans;
int main(){
cin>>x>>n>>m;
for(int i=1;i<=n;i++)
cin>>a[i];
sort(a+1,a+n+1);
for(int i=2;i<=n;i++)
b[i-1]=a[i]-a[i-1];
sort(b+1,b+n);
for(int i=n-m;i>=1;i--)
ans+=b[i];
cout<<ans;
}
5
5.1 题目描述 ：
“鲁迅说的话关我周树人什么事，文则打游戏关我高某人什么事。“
WZ 最近迷恋上了塔防益智小游戏，目标是尽可能多的净化敌方的区域，整个地图由“*”构成，敌方的地盘用“#”表示。每块敌方的地区 WZ 都需要派遣一位白骑士去净化，但是敌方为了保护自己的地盘建立了多个碉堡，每个碉堡用“!”表示。WZ 只能攻占一片敌方的区域，而这片区域每拥有一个碉堡 WZ 就需要多派一个白骑士去净化。问 WZ 想要尽可能多的净化敌方区域至少需要派遣多少个白骑士。
一曲忠诚的赞歌~
5.2 输入格式
\(\boxed{\begin{align}&n\ \ \ \ \ \ \ m\\&ch_{11}ch_{12}\dots ch_{1m}\\&ch_{21}ch_{22}\dots ch_{2m}\\ &\vdots\\ &ch_{n1}ch_{n2}\dots ch_{nm}\end{align}}\) 第一行，输入两个整数 \(n\) 和 \(m\) 代表整张地图的大小 接下来 \(n\) 行，每行将输入 \(m\) 个字符代表当前位置情况 \(1\leq n,m\leq 500\) ### 5.3 输出格式 \(\boxed{\begin{align}&x&y\end{align}}\) \(x\) 代表 WZ 可以占领的敌方区域大小，\(y\) 代表 WZ 至少需要派遣多少个白骑士
5.4 样例
输入 1
2
3
4
53 3
#!**
!#**
*#*#
*#*!1
6 8
题解：宽搜/深搜 1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
using namespace std;
int n,m;
char c[maxn][maxn];
int ti[4]={1,-1,0,0};
int tj[4]={0,0,1,-1};
bool v[maxn][maxn];
int ans1=0,ans2=0;
struct node{
int x,y;
};
void find(int a,int b){//搜索
int nans1=1,nans2=1;
if(c[a][b]=='!')nans2++;
v[a][b]=false;
queue<node> Q;
node X;
X.x=a,X.y=b;
Q.push(X);
while(!Q.empty()){
node fi=Q.front();
Q.pop();
int x=fi.x,y=fi.y;
for(int i=0;i<4;i++)
if(v[x+ti[i]][y+tj[i]]){
nans1++;nans2++;
if(c[x+ti[i]][y+tj[i]]=='!')nans2++;
node N;
N.x=x+ti[i],N.y=y+tj[i];
Q.push(N);
v[x+ti[i]][y+tj[i]]=false;
}
}
if(nans1>ans1){
ans1=nans1;
ans2=nans2;
}
}
int main(){
memset(v,false,sizeof(v));
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++){
cin>>c[i][j];
if(c[i][j]=='*')v[i][j]=false;
else v[i][j]=true;
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(v[i][j])find(i,j);
cout<<ans1<<" "<<ans2;
}